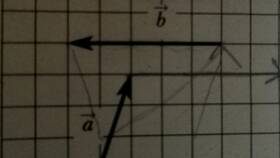Длина суммы векторов - это числовая характеристика, показывающая модуль (абсолютное значение) результирующего вектора, полученного при сложении двух или более векторов. Это важное понятие в векторной алгебре, имеющее широкое применение в физике, инженерии и компьютерной графике.
Содержание
Длина суммы векторов - это числовая характеристика, показывающая модуль (абсолютное значение) результирующего вектора, полученного при сложении двух или более векторов. Это важное понятие в векторной алгебре, имеющее широкое применение в физике, инженерии и компьютерной графике.
Основные понятия
Перед рассмотрением длины суммы векторов необходимо определить ключевые понятия:
- Вектор - направленный отрезок, характеризующийся длиной и направлением
- Длина вектора (модуль) - скалярная величина, обозначаемая как |v|
- Сумма векторов - результат операции сложения векторов по правилу треугольника или параллелограмма
Формула длины суммы двух векторов
Для двух векторов a и b длина их суммы вычисляется по формуле:
|a + b| = √(|a|² + |b|² + 2|a||b|cosθ)
где θ - угол между векторами a и b.
| Случай | Формула длины суммы |
| Коллинеарные векторы (θ = 0°) | |a + b| = |a| + |b| |
| Перпендикулярные векторы (θ = 90°) | |a + b| = √(|a|² + |b|²) |
| Противоположно направленные (θ = 180°) | |a + b| = ||a| - |b|| |
Свойства длины суммы векторов
Основные свойства
- Неравенство треугольника: |a + b| ≤ |a| + |b|
- Квадрат длины суммы: |a + b|² = |a|² + |b|² + 2(a·b)
- Для n векторов: |v₁ + v₂ + ... + vₙ| ≤ |v₁| + |v₂| + ... + |vₙ|
Геометрическая интерпретация
Длина суммы векторов соответствует:
- Диагонали параллелограмма, построенного на этих векторах (для двух векторов)
- Замыкающей стороне многоугольника при последовательном сложении
- Расстоянию от начала первого вектора до конца последнего
Практическое применение
Примеры вычислений
| Вектор a | Вектор b | Длина суммы |
| |a| = 3, θ = 0° | |b| = 4 | 3 + 4 = 7 |
| |a| = 5, θ = 90° | |b| = 12 | √(25 + 144) = 13 |
| |a| = 6, θ = 120° | |b| = 8 | √(36 + 64 + 2×6×8×(-0.5)) ≈ 7.21 |
Применение в физике
- Расчет результирующей силы в механике
- Определение суммарной скорости
- Вычисление напряженности электрического поля
- Анализ сложных движений в кинематике
Важные замечания
При вычислении длины суммы векторов следует учитывать:
- Угол между векторами существенно влияет на результат
- Длина суммы не равна сумме длин (кроме коллинеарного случая)
- Для трех и более векторов вычисления усложняются
