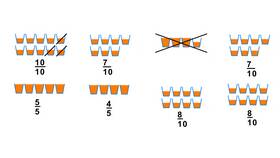
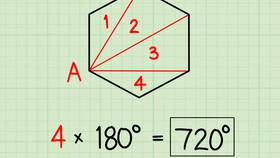
Сумма дробей - это результат сложения двух или более дробных чисел. Правила сложения дробей зависят от их вида (обыкновенные или десятичные) и от того, имеют ли дроби одинаковые или разные знаменатели.
Содержание
Сумма дробей - это результат сложения двух или более дробных чисел. Правила сложения дробей зависят от их вида (обыкновенные или десятичные) и от того, имеют ли дроби одинаковые или разные знаменатели.
Сложение обыкновенных дробей
Для сложения обыкновенных дробей существуют следующие правила:
Дроби с одинаковыми знаменателями
Если знаменатели дробей одинаковы, то:
- Числители складываются
- Знаменатель остается прежним
- Формула: a/b + c/b = (a + c)/b
| Пример: | 3/7 + 2/7 = (3+2)/7 = 5/7 |
Дроби с разными знаменателями
Если знаменатели разные, необходимо:
- Найти наименьший общий знаменатель (НОЗ)
- Привести дроби к общему знаменателю
- Сложить числители
- Знаменатель оставить без изменения
| Пример: | 1/4 + 1/6 = 3/12 + 2/12 = 5/12 |
Сложение смешанных чисел
Для сложения смешанных чисел (целая часть + дробь):
- Сложить целые части
- Сложить дробные части по правилам сложения дробей
- Если при сложении дробных частей получилась неправильная дробь, выделить целую часть
| Пример: | 2 1/3 + 3 1/2 = (2+3) + (1/3+1/2) = 5 + 5/6 = 5 5/6 |
Сложение десятичных дробей
Для сложения десятичных дробей:
- Записать дроби столбиком (запятая под запятой)
- Уравнять количество знаков после запятой, добавив нули
- Выполнить сложение как с натуральными числами
- Поставить запятую в сумме под запятыми в слагаемых
| Пример: | 3.25 + 0.478 = 3.250 + 0.478 = 3.728 |
Основные свойства сложения дробей
- Коммутативность: a + b = b + a
- Ассоциативность: (a + b) + c = a + (b + c)
- Существование нуля: a + 0 = a
Правильное сложение дробей требует внимательности и соблюдения всех математических правил. Особенно важно правильно находить общий знаменатель для обыкновенных дробей и аккуратно работать с запятыми при сложении десятичных дробей.
