В геометрии сумма внешних углов многоугольника является важной характеристикой, которая имеет постоянное значение для любых выпуклых многоугольников независимо от количества их сторон.
Содержание
Основная теорема о сумме внешних углов
Для любого выпуклого n-угольника сумма внешних углов, взятых по одному при каждой вершине, равна 360 градусам.
| Тип многоугольника | Сумма внешних углов |
| Треугольник | 360° |
| Четырехугольник | 360° |
| Пятиугольник | 360° |
| n-угольник | 360° |
Доказательство теоремы
Рассмотрим выпуклый n-угольник. В каждой вершине:
- Внутренний угол + Внешний угол = 180° (как смежные углы)
- Сумма всех внутренних углов равна (n-2)×180°
- Общая сумма всех внутренних и внешних углов будет n×180°
- Вычитая сумму внутренних углов, получаем сумму внешних углов: n×180° - (n-2)×180° = 360°
Примеры расчета
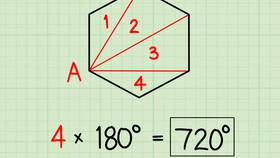
Пример 1: Правильный шестиугольник
- Каждый внутренний угол = 120°
- Каждый внешний угол = 180° - 120° = 60°
- Сумма внешних углов = 6 × 60° = 360°
Пример 2: Прямоугольник
- Каждый внутренний угол = 90°
- Каждый внешний угол = 180° - 90° = 90°
- Сумма внешних углов = 4 × 90° = 360°
Особые случаи
Невпуклые многоугольники
Для невыпуклых многоугольников сумма внешних углов также равна 360°, если учитывать знаки углов (положительные для поворотов против часовой стрелки и отрицательные - по часовой).
Многоугольники с отверстиями
Для многоугольников с отверстиями сумма внешних углов может отличаться от 360° и зависит от конкретной конфигурации фигуры.
Заключение
Сумма внешних углов выпуклого многоугольника всегда равна 360 градусам, независимо от количества его сторон. Это фундаментальное свойство широко используется в геометрии и инженерных расчетах.