В геометрии существует фундаментальное свойство треугольников, касающееся суммы их внутренних углов. Это свойство является важной теоремой в планиметрии.
Содержание
В геометрии существует фундаментальное свойство треугольников, касающееся суммы их внутренних углов. Это свойство является важной теоремой в планиметрии.
Основная теорема
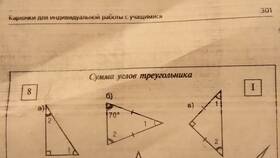
Сумма внутренних углов любого треугольника равна 180 градусам. Это утверждение справедливо для всех типов треугольников, независимо от их формы и размера.
Доказательство теоремы
- Рассмотрим произвольный треугольник ABC
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при вершине B составят развернутый угол (180°)
- Эти углы равны соответствующим углам треугольника при вершинах A и C
- Таким образом, сумма углов A, B и C равна 180°
Примеры расчета
| Тип треугольника | Углы | Сумма |
| Равносторонний | 60° + 60° + 60° | 180° |
| Прямоугольный | 90° + 45° + 45° | 180° |
| Произвольный | 70° + 60° + 50° | 180° |
Практическое применение
- Определение неизвестного угла треугольника, когда известны два других
- Проверка корректности построения треугольников
- Решение задач на построение в геометрии
- Применение в тригонометрических расчетах
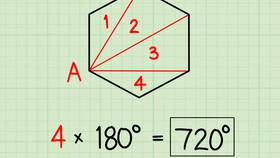
Исключения и особые случаи
Теорема о сумме углов треугольника справедлива только для евклидовой геометрии. В неевклидовых геометриях (например, сферической) сумма углов треугольника может отличаться от 180 градусов.
Знание этой теоремы является базовым для дальнейшего изучения геометрии и находит применение во многих областях математики и ее приложений.
